
De Amerikaanse onderzoeker, Phil Daro, vond bij het vergelijken van video’s van de Amerikaanse en de Japanse lessen een opvallend verschil. Wanneer Amerikaanse leraren een nieuwe opgave tegen kwamen, vroegen ze zich af, “Hoe kan ik ervoor zorgen dat mijn leerlingen deze opgaven kunnen maken?” De Japanse leraren stelden zichzelf een andere vraag, “Over welke wiskunde gaat dit en hoe kan ik mijn leerlingen deze wiskunde leren?” Deze twee reacties kunnen model staan voor het verschil in manieren waarop algemeen-georiënteerde onderwijsonderzoekers en vakdidactici tegen wiskundeonderwijs aankijken. De eersten richten zich veelal op de vraag, hoe je ervoor zorgt dat leerlingen bepaalde opgaven gaan beheersen. Bij de laatsten staat de vraag centraal, hoe de leerlingen zich de onderliggende wiskunde eigen kunnen maken. Dit leidt tot zeer verschillende conclusies over wat goed onderwijs is.
In dit artikel beschrijven we, waar die verschillen precies uit bestaan. Dit blijkt nodig omdat er in Nederland een breed gedeelde opvatting over onderwijs is ontstaan, waarbinnen voor het leren van wiskunde geen ruimte is.
Op dit moment is de trend in onderwijsland om je te laten leiden door wat je generaliserend onderwijsonderzoek zou kunnen noemen. Dat is onderzoek waarbij over verschillende leerstofinhouden en verschillende typen leerlingen wordt gegeneraliseerd. De gedachte daarbij is dat je resultaten van allerlei kwantitatief vergelijkend onderzoek samen kunt nemen. Je kijkt dan of je verbanden kunt vinden, zonder daarbij onderscheid te maken naar leerstofgebieden, leerlingen, of schooltypen. Het idee is dat je op die manier kunt vaststellen hoe hét beste onderwijs eruitziet. Maar, dat er één onderwijsmodel zou bestaan dat het beste zou werken voor elke onderwijssituatie, lijkt gezien de grote variëteit en complexiteit van het onderwijs onwaarschijnlijk. Daar komt nog eens bij dat het meest-aangehaalde onderzoek op dit gebied, dat van Hattie, van slechte kwaliteit is (Zo levert Slavin, expert op het gebied van meta-onderzoek, stevige kritiek. Zie Dolf Janson, “Wat klopt er niet bij John Hattie?”).
Dat de aanbevelingen die dit type onderzoek oplevert toch zo gemakkelijk ingang vinden, heeft waarschijnlijk te maken met het feit dat ze heel aannemelijk klinken. Of misschien is het andersom en zijn de aanbevelingen die veel worden genoemd, de aanbevelingen die het meest aannemelijk worden gevonden. In ieder geval worden deze opvattingen zo vaak herhaald, dat een collectief frame is ontstaan van, “Iedereen weet toch dat dit de kenmerken van goed onderwijs zijn”.
Maar vakdidactisch gezien zijn dit helemaal geen kenmerken van goed reken-wiskundeonderwijs!
In dit artikel bespreken we waarom rekenen-wiskunde niet binnen dit collectieve frame past.
Contrasterende kenmerken
Laten we eerst kijken wat zoal wordt genoemd als bewezen effectieve kenmerken van goed onderwijs. Dit betreft onder meer:
a) Leerstof moet worden opgebouwd van eenvoudig naar complex.
b) Eerst moet de noodzakelijke voorkennis worden aangebracht.
c) De leerlingen moeten weten wat de doelen zijn.
d) De leraar moet (goed) uitleggen, voordoen en laten oefenen.
e) De leerlingen moeten regelmatig feedback krijgen op wat ze goed of fout doen.
f) De verantwoordelijkheid voor de uitvoering moet geleidelijk worden overdragen van de leraar naar de leerling.

We kunnen dit contrasteren met hoe er in vakdidactische kring, nationaal en internationaal, wordt gedacht over reken-wiskunde onderwijs:
a) Leergangen moeten een ontwikkeling mogelijk maken die verloopt van informeel (vertrouwd) naar formeel (abstract).
b) De informele kennis van de leerlingen moet het startpunt zijn.
c) Er moet onderscheid worden gemaakt tussen doel van de leraar en het doel voor de leerling.
d) De leraar moet het denkwerk bij de leerlingen leggen.
e) Leraren moeten opdrachten aanbieden, die het gewenste denken van de leerlingen uit kunnen lokken, vervolgens analyseren hoe de leerlingen denken, en daarop inspelen.
f) Leerlingen moeten beseffen, dat ze hun antwoorden moeten kunnen onderbouwen.
Deze kenmerken van vakdidactisch georiënteerd reken-wiskundeonderwijs vinden hun oorsprong in het abstracte karakter van rekenen-wiskunde. We hebben namelijk te maken met een wiskundige werkelijkheid die losstaat van de alledaagse werkelijkheid. Dit komt, bijvoorbeeld, naar voren in de manier waarop we het oplossen van toepassingsproblemen karakteriseren. Daarbij onderscheiden we de volgende stappen;
het vertalen van het probleem in de werkelijkheid naar een (reken-)wiskundig probleem,
het oplossen van dit reken-wiskundige probleem met (reken-)wiskundige middelen,
het terugvertalen van de oplossing naar de oorspronkelijke probleemsituatie en
het controleren of het oorspronkelijke probleem hiermee is opgelost.
Je zou kunnen zeggen dat je in het oplossingsproces heen-en-weer gaat tussen de concrete werkelijkheid en de wiskunde (In dit betoog gaan we ervan uit dat de wiskunde het rekenen omvat). Eerst ga je van de werkelijkheid naar de wiskunde, dan los je het probleem binnen de wiskunde op en met die oplossing ga je terug naar de ‘gewone’ werkelijkheid. Deze beschrijving laat het bijzondere karakter van wiskunde zien. Je hebt als het ware twee lagen, de concrete werkelijkheid en de wiskundige werkelijkheid.
Leren van rekenen-wiskunde
Om erachter te komen hoe zo’n wiskundige werkelijkheid ontstaat kun je kijken naar de geschiedenis van de wiskunde. Onderzoek van Anna Sfard (1991) heeft laten zien dat de geschiedenis van de wiskunde wordt gekenmerkt door een opeenvolging van cycli, waarin processen het karakter krijgen van objecten, die weer onderwerp van nieuwe processen worden. Ze spreekt in dit verband van reification, letterlijk, “verdinglijking”. Veel experts op het gebied van reken-wiskundeonderwijs verwijzen naar een dergelijk fenomeen, zij het soms in andere termen (Tall, Dubinsky, Cobb, Freudenthal, Pirie, Kieren). Sfard wijst er daarbij op dat deze objectvorming niet absoluut is, de verbinding met het oorspronkelijke proces blijft bestaan. Een van de kenmerken is juist dat je heen-en-weer kunt tussen proces en object. Ze spreekt daarom van dualiteit, wiskundige begrippen hebben altijd twee kanten, een proceskant en een objectkant.
Functies als voorbeeld
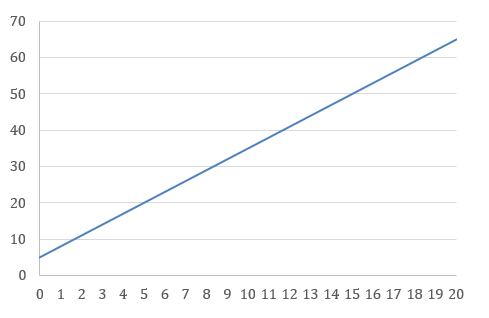
Een van de voorbeelden die ze geeft betreft het begrip functie. Het blijkt dat functies eerst naar voren komen als proces. Een formule als f(x) = 3x + 5 wordt dan gelezen als een rekenvoorschrift, wat luidt: ‘vermenigvuldig het input-getal met 3 en tel er daarna 5 bij op’. Wanneer we dit rekenvoorschrift op een reeks van waarden toepassen, kun je een patroon ontdekken. Als de input-getallen toenemen, nemen de output-getallen ook toe én er is sprake van een regelmatige toename. Dit patroon wordt goed zichtbaar als je de grafiek van f(x) = 3x + 5 tekent.
(f)x
 x
x
Grafiek van f(x) = 3x + 5 voor positieve x.
We hebben dan onze blik verlegd van individuele gevallen naar de verzameling in- en output-getallen. Meer formeel, kunnen we de functie f(x) = 3x + 5 definiëren als de verzameling getallenparen (x, y) die aan het voorschrift y = 3x + 5 voldoen. De functie f(x) = 3x + 5 is nu een object geworden. Een object met bepaalde kenmerken. In dit geval is dat het lineaire karakter van deze functie. Daarmee onderscheidt de lineaire functie zich van functies die een ander karakter hebben, zoals kwadratisch of periodiek.
Natuurlijke getallen
Andere voorbeelden van wiskundige objecten zijn natuurlijke getallen en breuken. Voor heel jonge kinderen zijn getallen nog gebonden aan telbare objecten. Het getal “vier” heeft alleen betekenis in de context van “vier blokjes”, “vier appels” etc. Na verloop van tijd krijgen deze getallen het karakter van wiskundige objecten die hun betekenis ontlenen aan getalrelaties als, “4 = 2 + 2”, “5 – 1 = 4”, “2 x 4 = 8” enz. De leerlingen construeren deze getalrelaties via het reflecteren op het splitsen, samennemen en vergelijken van hoeveelheden. Zo gaan de leerlingen inzien dat vier plus vier” altijd “acht” oplevert. Anders gezegd, ze construeren de relatie “4 + 4 = 8” als onderdeel van een nieuwe wiskundige wereld.
Breuken
De leerlingen leren breuken eerst kennen als benoemde getallen, “¼ pizza”, “¾ reep” etc. In onderwijs dat zich daarop richt kunnen leerlingen breuken gaan zien als onbenoemde getallen. Ofwel, wiskundige objecten die hun betekenis ontlenen aan getalrelaties. In het geval van ¾ zijn kunnen we, bijvoorbeeld, denken aan relaties als,
|
3 ÷ 4 = ¾ ¾ = 3 x ¼ ¾ = 1 – ¼ ¾ = ½ + ¼ ¾ + ¾ = 1 ½ ¾ = 6/8 enz. |
Deze relaties komen naar voren in activiteiten als vergelijken, samennemen, afhalen enzovoort in de context van verdelen, meten, verhoudingen en dergelijke. De overgang naar formele, onbenoemde breuken is echter niet gemakkelijk. Vooral niet als het rekenen met breuken sterk leunt op regels en procedures en getalrelaties weinig aandacht krijgen.
Vakdidactici gaan er in het algemeen vanuit dat leerlingen een vergelijkbare ontwikkeling moeten doorlopen om betekenisvolle wiskunde te kunnen ontwikkelen. Leerlingen krijgen dan een actieve rol in het reflecteren op wiskundige processen en het construeren van wiskundige objecten. Vanuit dit perspectief kunnen we de bovengenoemde kenmerken toelichten.
a) Leergangen moeten een ontwikkeling mogelijk maken die verloopt van informeel (vertrouwd) naar formeel (abstract).
Dit is in wezen de kern van het betoog hierboven. Wiskunde kun je niet in de abstracte, formele, vorm overdragen waarin wij deze wiskunde kennen. Leerlingen moeten een proces doormaken waarbij de informele kennis waar ze over beschikken, wordt uitgebouwd naar de formele wiskunde die wordt beoogd. Hiertoe moet een leerroute worden uitgezet die dit mogelijk maakt. Dit is geen sinecure. Om geschikte leergangen te ontwikkelen wordt daarom ontwerponderzoek uitgevoerd.
b) De informele kennis van de leerlingen moet het startpunt zijn.
Je kunt de wiskunde van volwassenen niet top-down verbinden met de concrete werkelijkheid van de leerlingen. Daarom wordt ervoor gekozen om goed aan te sluiten bij wat de leerling al weet en begrijpt. Startpunten worden daarom gezocht in probleemsituaties die experientially real zijn voor de leerlingen. Dat zijn situaties waarbinnen de leerlingen betekenisvol kunnen handelen en redeneren. Dit kunnen situaties uit de werkelijkheid zijn, fantasiesituaties, of bestaan uit al bekende wiskunde. Deze situaties worden zo gekozen dat ze als startpunt kunnen dienen voor het ontwikkelen van de beoogde wiskunde.
Anders gezegd, je zoekt vanuit wat de leerling al weet en begrijpt, naar een mogelijke leerroute. In plaats van het eindpunt als uitgangspunt te kiezen en daar de beginvoorwaarden bij te zoeken.

c) Er moet onderscheid worden gemaakt tussen het doel van de leraar en het doel voor de leerling.
Dit onderscheid vormt de achtergrond van de observatie van Phil Daro. Het doel van de leraar is de leerlingen te helpen bij het ontwikkelen van wiskunde. Het maken van, reflecteren op en discussiëren over, bepaalde opgaven is hiervoor het middel. Voor de leerlingen is het beantwoorden van de opgaven het doel. Het wiskundige doel dat de leraar beoogt is te abstract, om voor de leerlingen als doel te kunnen dienen.
d) De leraar moet het denkwerk bij de leerlingen leggen.
In de vakdidactiek wordt ervan uitgegaan dat leerlingen zich betekenisvolle wiskunde alleen eigen kunnen maken via probleem oplossen, reflecteren en redeneren. Dit staat haaks op uitleggen en voordoen. Bovendien zal het oefenen steeds zo worden ingericht, dat ook hier denken aan te pas komt.
e) Leraren moeten opdrachten aanbieden die het gewenste denken van de leerlingen uit kunnen lokken, vervolgens analyseren hoe de leerlingen denken, en daarop inspelen.
Als je ervan uitgaat dat je rekenen-wiskunde niet in een kant-en-klare vorm kunt overdragen moet de leraar de reken-wiskundige ontwikkeling van de leerlingen op een meer indirecte manier sturen. Dit kan door te anticiperen op hoe de leerlingen zullen denken wanneer ze aan de slag gaan met de opgave die je aanbiedt. En hoe deze denkactiviteit kan bijdragen tot het doel dat je wilt bereiken. Uiteraard moet je daarbij als leraar in het oog houden, of het denken van de leerlingen wel zo verloopt als je had verwacht.
f) Leerlingen moeten beseffen, dat ze hun antwoorden moeten kunnen onderbouwen.
In reken-wiskundeonderwijs volgens het model van uitleggen-voordoen-oefenen-feedback is de leraar de bron van alle kennis. Leerlingen worden geacht te doen wat de leraar aangeeft. Van de leraren wordt verwacht dat zij heldere uitleg en adequate feedback geven. Het is niet aan de leerling om te bepalen wat juist of niet juist is, dat dient te worden overgelaten aan de leraar.
In op wiskundige ontwikkeling gericht reken-wiskundeonderwijs zijn de rollen anders verdeeld. Van de leerlingen wordt verwacht dat ze zelf nadenken, hun oplossingen kunnen onderbouwen en daarover met anderen in discussie gaan. Leraren stellen zich terughoudend op en proberen het leerproces te sturen via vragen, opdrachten en klassendiscussies.
Besluit
Over wat het doel van reken-wiskundeonderwijs is, kan verschillend worden gedacht. Het wordt echter problematisch, als er uit het oog wordt verloren dat er verschillende opvattingen zijn. In Nederland is het idee dat het bij rekenen-wiskunde gaat om het leren van procedures zo dominant dat het alleen nog maar lijkt te gaan over de vraag, hoe je die procedures zo effectief mogelijk kunt leren. De meeste vakdidactici vinden echter dat het reken-wiskundeonderwijs zou moeten gaan over de wiskunde achter deze procedures. Dit betekent niet dat de leerlingen geen procedures meer zouden moeten leren. Maar procedures zonder wiskundige basis hebben weinig waarde. Zeker in een tijd waarin steeds meer procedures aan apparaten worden overgelaten. Het reken-wiskundeonderwijs moet zich richten op wat echt belangrijk is en niet aan de leiband (blijven) lopen van wat generaliserend onderwijsonderzoek ons leert.

Koeno Gravemeijer is emeritus professor science- en techniekeducatie aan de Technische Universiteit Eindhoven. Foto: Bart van Overbeeke
Een ingekorte versie van dit artikel verscheen in Didactief, maart 2022.
Wil je meer lezen over Anna Sfard en het proces- en het objectkarakter van wiskundige concepten, surf dan naar ‘Een internationaal perspectief op reken- en wiskundeonderwijs Nr. 1, over Sfard’ (1991). Meer informatie over Gray en TAll en hetzelfde thema, lees je in Een internationaal perspectief op reken- en wiskundeonderwijs Nr. 2, over Gray en Tall (1994) . Beide artikelen zijn verschenen op de website van de werkgroep Wiskunde voor Morgen, een gezamenlijke werkgroep van de NVvW en de NVORWO.
1 PISA 2021 Mathematics Framework
2 Mastery learning, dat was toch passé?
3 Reken- en Wiskundeonderwijs voor #2032
4 Tijd voor ander rekenonderwijs
5 Waar moet de reken/wiskundeles straks over gaan?
6 Wat heb je aan onderzoek over wat werkt?
7 Over (wiskunde)onderwijs
En blijf op de hoogte van onderwijsnieuws en de nieuwste wetenschappelijke ontwikkelingen!
Inschrijven