Grow staat voor Gedifferentieerd RekenOnderWijs. De essentie is een stappenplan: stel onderwijsbehoeften vast, stel doelen, differentieer de instructie en de verwerking, en evalueer proces en voortgang. Per stap beschrijven we in dit artikel wat dit voor sterke rekenaars betekent.
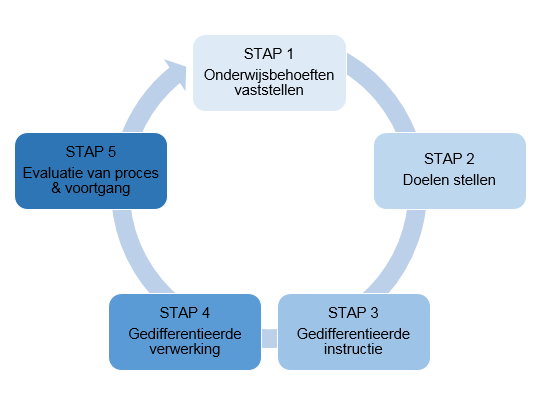
Eerste stap is het in kaart brengen van wat leerlingen kennen en kunnen. Je maakt een grove indeling in subgroepen op basis van scores op Cito rekenen-wiskunde en op de methode gebonden toetsen. Die indeling kan in de loop van het jaar veranderen en per (sub)domein kan een kind verschillend worden ingedeeld. Vervolgens analyseer je toetsopgaven en leerlingwerk, de categorieënanalyse, diagnostische gesprekken, observatiesystemen en peilingspelletjes. Soms presteert een leerling ondanks hoge Cito-scores onvoldoende op de methodetoetsen. Oorzaak is vaak een gebrek aan motivatie. Praat er over met de leerling en zoek samen naar een passend rekenaanbod.
Sterke rekenaars maken grote denksprongen, zien snel wiskundige structuren en patronen, zijn goed in het leggen van verbanden en verwerken de rekenstof sneller. Soms is het daarom lastig om tussenstappen expliciet te maken. Het is verstandig om dit toch extra met ze te oefenen, omdat juist dit in het voortgezet onderwijs wordt gevraagd.
Vaak zien sterke rekenaars het nut van automatiseren en memoriseren niet in. Het uitrekenen geeft hen meer voldoening, maar kost meer ruimte in het werkgeheugen. Dat kan ze later in de problemen brengen. Leg dan ook het doel van automatiseren en memoriseren uit.
Sterke rekenaars leren zelden effectieve oplossingsstrategieën te zoeken. Om ze te leren leren, hun doorzettingsvermogen te oefenen en onderpresteren te voorkomen, hebben zij voldoende, niet-vrijblijvende uitdaging (mét begeleiding) nodig.
Geef ze opgaven die open, betekenisvol en complex zijn en die een onderzoekende houding uitlokken, uitnodigen tot reflectie en stimuleren om op een hoger abstractieniveau te denken. Stimuleer hun creatief denkvermogen. Een bruikbaar model is bijvoorbeeld de bekende taxonomie van Bloom.
Wie bewust omgaat met het doel van de les, kan instructie, werkvormen en ondersteunende materialen beter op elkaar afstemmen. Hoewel steeds meer nieuwe rekenmethoden op drie niveaus lesdoelen formuleren, is het jouw taak als leerkracht om deze doelen (haalbaar en uitdagend) te formuleren.
De leerdoelen voor sterke rekenaars zijn op te delen in drie categorieën: goede beheersing van de reguliere stof, rekeninhoudelijke verrijking en zelfregulatie. Juist deze kinderen moeten efficiënte oplossingsstrategieën leren gebruiken en rekenconcepten ontwikkelen. De doelen moeten helder geformuleerd zijn, op schoolniveau, op subgroepniveau en op het niveau van de individuele leerling: Welk prestatieniveau wordt verwacht van sterke rekenaars? Welke onderliggende concepten moeten zij beheersen? Welke oplossingsstrategieën moeten zij beheersen en toepassen? En zijn dit dezelfde als de strategieën die de methode aanreikt?
Het formuleren van rekeninhoudelijke verrijkingsdoelen voorkomt dat de verwerkingsstof onvoldoende uitdagend is en te veel overlap vertoont met de reguliere doelen van een hoger leerjaar.
Je kunt met een klassikale instructie en tijdens extra instructie aan kleinere groepen variëren in tempo en hoeveelheid, maar ook in het gebruik van de handelingsniveaus, de moeilijkheidsgraad, het soort vragen dat je stelt, de mate van sturing en begeleiding die je geeft, en de aanwezigheid en aard van de interactie.
Voor sterke rekenaars moet er voldoende uitdaging in de opdrachten en vragen zitten. Door ze over strategieën te laten discussiëren (Waarom doe jij het zo?), en ze aan te zetten tot kritisch denken en argumenteren (Waarom is dat eigenlijk zo?) doe je een beroep op hun reflectieve en metacognitieve vaardigheden. Besteed veel aandacht aan het proces: het gaat er vooral om hoe zij tot hun antwoord komen. Maak daarnaast expliciet duidelijk dat ze fouten mogen maken. Bespreek de gekozen aanpak, bijvoorbeeld door minimaal twee keer per week een kwartier rekeninhoudelijke begeleiding te geven.
Als leerlingen zelfstandig aan het werk gaan, moeten ook de verwerkingsopdrachten zijn aangepast: de hoeveelheid verwerkingsstof , de verwerkingsvorm (bijvoorbeeld discussies of een mindmap), en de manier waarop de verwerkingsstof gepresenteerd wordt (formele symbolen versus plaatjes).
Je kunt het verwerkingsaanbod aanpassen met compacten en verrijken. Compacten is het indikken van de leerstof tot de essentie zonder herhaling. Als je twijfelt over compacten, kun je leerlingen al vóór het blok begint de methodetoets laten maken. Zo krijg je zicht op de aanwezige kennis. Hoewel de nieuwere rekenmethoden doorgaans onderscheid maken in de rekenleerstof voor drie subgroepen, moet je zelf beoordelen welke stof ingedikt kan worden.
Kinderen die minder rekenopdrachten maken, houden tijd over. Verrijkingsopdrachten zoals Kien, Rekentijgers, of opdrachten uit Acadin, Levelwerk, Nieuwsrekenen, Prof dr Testkees bieden dan extra uitdaging. Je kunt ook opdrachten uit de rekenmethode aanpassen. Betrek leerlingen wel bij de keuze van verrijkingsmateriaal. Denk na over de moeilijkheidsgraad, de mate waarin ze een beroep doen op de vaardigheden die de leerlingen moeten ontwikkelen en praktische zaken, zoals hoeveel instructietijd de materialen zullen vergen. Hieronder vind je zeven verrijkingsprincipes om de geschiktheid van verrijkingsopdrachten te beoordelen of zelf rekenopdrachten uit de methode rijker te maken.
Spreek wel af wat de leerling minimaal af moet hebben aan het einde van een periode. Begeleid hem, ook bij het zelfstandig leren plannen en werken. Leg aan de klas uit waarom sterke rekenaars opgaven overslaan en andere opgaven maken. Vermeld verrijkingsopdrachten in het rapport.
Waren de gekozen aanpakken effectief ? De volgende subvragen staan centraal: Sloten de instructie en verwerking aan bij de onderwijsbehoeften van de leerlingen? Hebben de leerlingen de (voor hen) gestelde doelen behaald? Op welke manier lossen leerlingen opgaven op: welk rekenproces gaat er schuil achter een bepaald (goed/fout) antwoord? En geeft dit aanwijzingen voor de instructie die in de toekomst nodig is?
Bij evaluatie gebruik je niet alleen periodieke toetsen. Ook tussentijds win je informatie in door rekenwerk na te kijken en observaties tijdens de les. Als leerlingen systematisch dezelfde fouten maken, kan je hier aandacht aan besteden in de volgende instructie. Daarmee is de cyclus van differentiatie weer rond en wordt een volgende cyclus in gang gezet.
Zie ook: Eva van de Weijer-Bergsma e.a., ‘Differentiëren in het rekenonderwijs’, Doetinchem: Graviant Scientific & Educational Books, 2016. Grow is ontwikkeld door Hogeschool Windesheim.
Sterke rekenaars op de basisschool kunnen profijt hebben van het compacten van de verwerkingsstof, het indikken van de leerstof tot de essentie zonder herhaling.
Als je twijfelt over compacten, kun je leerlingen al vóór een blok begint de methodetoets laten maken. Zo krijg je zicht op de aanwezige kennis. Hoewel de nieuwere rekenmethoden doorgaans onderscheid maken in de rekenleerstof voor drie subgroepen, moet je zelf beoordelen welke stof ingedikt kan worden.
Verrijkingsopdrachten zoals Kien, Rekentijgers, of opdrachten uit Acadin, Levelwerk, Nieuwsrekenen, Prof dr Testkees bieden extra uitdaging. Je kunt ook opdrachten uit de rekenmethode aanpassen. Betrek leerlingen wel bij de keuze van verrijkingsmateriaal. Denk na over de moeilijkheidsgraad, de mate waarin ze een beroep doen op de vaardigheden die de leerlingen moeten ontwikkelen en praktische zaken, zoals hoeveel instructietijd de materialen zullen vergen. Hieronder vind je zeven verrijkingsprincipes om de geschiktheid van verrijkingsopdrachten te beoordelen of zelf rekenopdrachten uit de methode rijker te maken.
De leerkracht / leerstof:
1. stelt een ander soort vragen (die meer open zijn);
2. geeft de opdracht een andere vorm (bijvoorbeeld door een spel, andere context, model of grafiek toe te voegen);
3. zorgt voor een grotere complexiteit (door leerlingen bijvoorbeeld meer gegevens te laten combineren);
4. verbindt rekenen met andere vakken (door in thema’s of projecten te werken);
5. laat eigen constructies en producties maken (zoals het bedenken van eigen opgaven of nieuwe spelregels bij een bestaand spel);
6. daagt uit tot reflectie en filosoferen (door goede vragen te stellen),
7. verbreedt het aanbod met domeinen en activiteiten (door bijvoorbeeld strategische spellen als schaken of bridge in te zetten).
Bron: Janson & Noteboom, Compacten en verrijken van de rekenles voor (hoog)begaafde leerlingen in het basisonderwijs. Enschede: SLO, 2004
En blijf op de hoogte van onderwijsnieuws en de nieuwste wetenschappelijke ontwikkelingen!
Inschrijven
